Формула силы притяжения

Формула для силы притяжения тел произвольной формы

В двух телах произвольной формы и размера выделим элементарные массы, которые можно считать материальными точками, причем:

где $\rho_1, \rho_2$ – плотности вещества материальных точек первого и второго тел,
dV₁ ,dV₂ — элементарные объемы выделенных материальных точек. В таком случае, сила притяжения
($d \bar{F}_12$), с которой элемент dm₂ действует
на элемент dm₁, равна:

Следовательно, сила притяжения первого тела вторым может быть найдена по формуле:

где интегрирование необходимо произвести по всему объему первого (V₁) и второго (V₂) тел.
Если тела являются однородными, то выражение можно немного преобразовать и получить:

Современная история изменений гравитационной постоянной

Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

По результатам команды первый метод продемонстрировал значение гравитационной постоянной

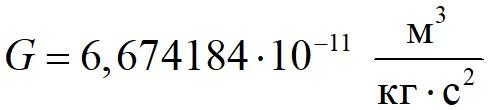
-6

Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

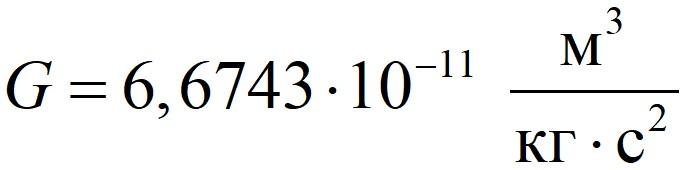
Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.

Формула силы притяжения между телами в космосе

Закономерность гравитации, которую обнаружил Ньютон, можно представить в виде математической формулы. Вычисления выглядят следующим образом:

\(F=G\times m1\times m2\times r^2\),

где \(m1,m2\) — массы объектов, которые притягиваются друг к другу под действием силы \(F\),

\(r\) – расстояние, на которое удалены тела,

\(G\) — т.н. гравитационная постоянная величина, константа, равная 6,67.

Гравитационное взаимодействие объектов будет слабеть, если тела удаляются друг относительно друга. Сила гравитации пропорциональна величине расстояния в квадрате. При этом для нахождения искомой величины расстояние измеряется от центров тяжести тел, а не от поверхностей.

Первая космическая скорость

Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

Определение Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

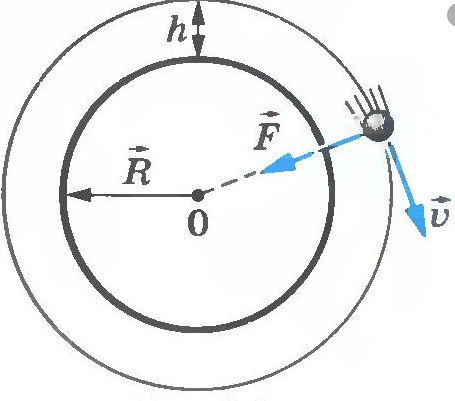
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙10 24 кг, а ее радиус равен 6052 км.

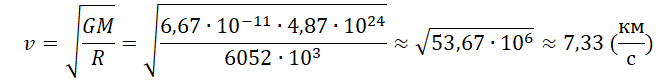
Алгоритм решения

1. Записать исходные данные.
2. Записать закон всемирного тяготения.
3. Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
4. На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.

Решение

Запишем исходные данные:

• Расстояние между двумя шарами в первом случае: R₁ = 2 м.
• Расстояние между двумя шарами во втором случае: R₂ = 6 м.
• Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.

Запишем закон всемирного тяготения:

Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m₁ и m₂.

R₂ больше R₁ втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 3 2 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

Источник

Определение и формула силы притяжения

Определение

Между любыми телами, которые обладают массами, действуют силы, которые притягивают вышеназванные тела друг к другу.
Такие силы называют силами взаимного притяжения.

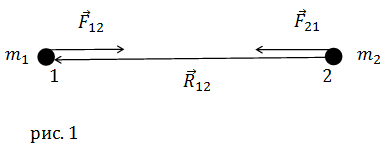
Рассмотрим две материальные точки (рис.1). Они притягиваются с силами прямо пропорциональными произведению масс этих материальных точек и
обратно пропорциональными расстоянию между ними. Так, сила тяготения (
$\bar{F}_12$) будет равна:

где материальная точка массы m₂ действует на материальную точку массы m₁ с силой притяжения
$\bar{F}_12$; $\bar{r}_12$ – радиус – вектор, который проведен из точки 2 в
точку 1, модуль этого вектора равен расстоянию между материальными точками (r); G=6,67•10-11 м3 кг-1
с-2(в системе СИ) – гравитационная постоянная (постоянная тяготения).

В соответствии с третьим законом Ньютона сила, с которой материальная точка 2 притягивается к материальной точке 1 (
$\bar{F}_21$) равна:

где $\bar{r}_12 = — \bar{r}_21$

Тяготение между телами осуществляется посредством гравитационного поля (поля тяготения). Силы тяготения являются потенциальными. Это дает возможность ввести такую энергетическую характеристику гравитационного поля как потенциал, который равен отношению потенциальной энергии материальной точки, находящейся исследуемой точке поля к массе данной точки.

Свойства ньютоновского тяготения

В ньютоновской теории каждое массивное тело порождает силовое поле притяжения к этому телу, называемое гравитационным полем. Это поле потенциально.

Гравитационное взаимодействие в теории Ньютона распространяется мгновенно, так как сила тяготения зависит только от взаимного расположения притягивающихся тел в данный момент времени. Также для ньютоновских гравитационных сил справедлив принцип суперпозиции: сила тяготения, действующая на частицу со стороны нескольких других частиц, равна векторной сумме сил притяжения со стороны каждой частицы. Сила тяготения сообщает всем телам одинаковое ускорение, независимо от массы, химического состава и других свойств тел (принцип эквивалентности).

В случае, если поле создаётся расположенной в начале координат точечной массой M{\displaystyle M}, функция гравитационного потенциала определяется формулой:

φ(r→)=−GMr{\displaystyle \varphi ({\vec {r}})=-G{\frac {M}{r}}},

при этом потенциал на бесконечности принят равным нулю.

В общем случае, когда плотность вещества ρ{\displaystyle \rho } распределена произвольно, φ{\displaystyle \varphi } удовлетворяет уравнению Пуассона:

Δφ(r→)=−4πGρ(r→){\displaystyle \Delta \varphi ({\vec {r}})=-4\pi G\rho ({\vec {r}})}.

Решение данного уравнения записывается в виде:

φ(r→)=−G∫V′ρ(r→′)dV′|r→−r→′|+C{\displaystyle \varphi ({\vec {r}})=-G\int _{V^{\prime }}{\frac {\rho ({\vec {r}}^{\prime })dV^{\prime }}{|{\vec {r}}-{\vec {r}}^{\prime }|}}+C}.

Здесь r→{\displaystyle {\vec {r}}} — радиус-вектор точки, в которой определяется потенциал, r→′{\displaystyle {\vec {r}}^{\prime }} — радиус-вектор элемента объёма dV′{\displaystyle dV^{\prime }} c плотностью вещества ρ(r→′){\displaystyle \rho ({\vec {r}}^{\prime })}, а интегрирование охватывает все такие элементы; C{\displaystyle C} — произвольная постоянная.

Сила притяжения, действующая в гравитационном поле на материальную точку с массой m{\displaystyle m}, связана с потенциалом формулой:

F→(r→)=−m∇φ(r→){\displaystyle {\vec {F}}({\vec {r}})=-m\nabla \varphi ({\vec {r}})}.

Если поле создаётся точечной массой M{\displaystyle M}, расположенной в начале координат, то на точку массой m{\displaystyle m} действует сила

F→(r→)=−GmMr3⋅r→{\displaystyle {\vec {F}}({\vec {r}})=-G{\frac {mM}{r^{3}}}\cdot {\vec {r}}}.

Величина этой силы зависит только от расстояния r{\displaystyle r} между массами, но не от направления радиус-вектора r→{\displaystyle {\vec {r}}} (см. формулу в преамбуле).

Сферически симметричное тело создаёт за своими пределами такое же поле, как материальная точка той же массы, расположенная в центре тела.

Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.

Исторический очерк

Закон всемирного тяготения Ньютона

Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире. Были, впрочем, догадки с правильной зависимостью от расстояния; Ньютон в письме к Галлею упоминает как своих предшественников Буллиальда, Рена и Гука. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).

В своём основном труде «Математические начала натуральной философии» () Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Он показал, что:

• наблюдаемые движения планет свидетельствуют о наличии центральной силы;
• обратно, центральная сила притяжения приводит к эллиптическим (или гиперболическим) орбитам.

Теория Ньютона имела ряд существенных отличий от гипотез предшественников. Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:

• закон тяготения;
• закон движения (второй закон Ньютона);
• система методов для математического исследования (математический анализ).

В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел и тем самым создаёт основы небесной механики. До Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить.

Отметим, что теория тяготения Ньютона уже не была, строго говоря, гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга.

В течение XVIII века закон всемирного тяготения был предметом активной дискуссии (против него выступали сторонники школы Декарта) и тщательных проверок. К концу века стало общепризнанным, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Генри Кавендиш в 1798 году осуществил прямую проверку справедливости закона тяготения в земных условиях, используя исключительно чувствительные крутильные весы. Важным этапом стало введение Пуассоном в 1813 году понятия гравитационного потенциала и уравнения Пуассона для этого потенциала; эта модель позволяла исследовать гравитационное поле при произвольном распределении вещества. После этого ньютоновский закон стал рассматриваться как фундаментальный закон природы.

В то же время ньютоновская теория содержала ряд трудностей. Главная из них — необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс. В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

Звания в ФСБ

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

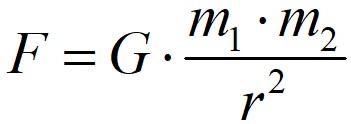
формула закона всемирного тяготения

G – коэффициент пропорциональности или гравитационная постоянная;

m_1, m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

значение гравитационной постоянной

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

гравитационная постоянная в законе всемирного тяготения

Электрооборудование

В качестве источников питания для грузовика выступают:

• генератор напряжением 28 В и мощностью до 2 тыс. Вт;
• две аккумуляторных батареи емкостью 190 А*ч.

Источники питания обеспечивают внутреннее сетевое напряжение 24 В.

Самосвал КамАЗ-65201

Исторический очерк

Закон всемирного тяготения Ньютона

Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире. Были, впрочем, догадки с правильной зависимостью от расстояния; Ньютон в письме к Галлею упоминает как своих предшественников Буллиальда, Рена и Гука. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).

В своём основном труде «Математические начала натуральной философии» () Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Он показал, что:

• наблюдаемые движения планет свидетельствуют о наличии центральной силы;
• обратно, центральная сила притяжения приводит к эллиптическим (или гиперболическим) орбитам.

Теория Ньютона имела ряд существенных отличий от гипотез предшественников. Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:

• закон тяготения;
• закон движения (второй закон Ньютона);
• система методов для математического исследования (математический анализ).

В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел и тем самым создаёт основы небесной механики. До Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить.

Отметим, что теория тяготения Ньютона уже не была, строго говоря, гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга.

В течение XVIII века закон всемирного тяготения был предметом активной дискуссии (против него выступали сторонники школы Декарта) и тщательных проверок. К концу века стало общепризнанным, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Генри Кавендиш в 1798 году осуществил прямую проверку справедливости закона тяготения в земных условиях, используя исключительно чувствительные крутильные весы. Важным этапом стало введение Пуассоном в 1813 году понятия гравитационного потенциала и уравнения Пуассона для этого потенциала; эта модель позволяла исследовать гравитационное поле при произвольном распределении вещества. После этого ньютоновский закон стал рассматриваться как фундаментальный закон природы.

В то же время ньютоновская теория содержала ряд трудностей. Главная из них — необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс. В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

Ограничения

Описание гравитации Ньютоном достаточно точное для многих практических целей и поэтому широко используется. Отклонения от него малы, когда безразмерные величины и обе намного меньше единицы, где — гравитационный потенциал , — скорость исследуемых объектов и — скорость света в вакууме. Например, ньютоновская гравитация дает точное описание системы Земля / Солнце, поскольку
ϕ c 2 {\ displaystyle \ phi / c ^ {2}} ( v c ) 2 {\ displaystyle (v / c) ^ {2}} ϕ {\ displaystyle \ phi} v {\ displaystyle v} c {\ displaystyle c}

ϕ c 2 знак равно грамм M s ты п р о р б я т c 2 ∼ 10 — 8 , ( v E а р т час c ) 2 знак равно ( 2 π р о р б я т ( 1   y р ) c ) 2 ∼ 10 — 8 {\ displaystyle {\ frac {\ phi} {c ^ {2}}} = {\ frac {GM _ {\ mathrm {sun}}} {r _ {\ mathrm {orbit}} c ^ {2}}} \ sim 10 ^ {- 8}, \ quad \ left ({\ frac {v _ {\ mathrm {Earth}}} {c}} \ right) ^ {2} = \ left ({\ frac {2 \ pi r _ {\ mathrm {орбита}}} {(1 \ \ mathrm {yr}) c}} \ right) ^ {2} \ sim 10 ^ {- 8}}

где — радиус орбиты Земли вокруг Солнца.
р орбита {\ displaystyle r _ {\ text {орбита}}}

В ситуациях, когда любой безразмерный параметр велик,
для описания системы необходимо использовать общую теорию относительности . Общая теория относительности сводится к ньютоновской гравитации в пределе малого потенциала и малых скоростей, поэтому закон тяготения Ньютона часто называют пределом низкой гравитации общей теории относительности.

Наблюдения, противоречащие формуле Ньютона

• Теория Ньютона не полностью объясняет прецессию перигелия орбит планет, особенно Меркурия, которая была обнаружена намного позже жизни Ньютона. Существует расхождение в 43 угловых секунды за столетие между расчетом Ньютона, которое возникает только из-за гравитационного притяжения других планет, и наблюдаемой прецессии, сделанной с помощью современных телескопов в 19 веке.
• Прогнозируемое угловое отклонение световых лучей под действием силы тяжести (рассматриваемое как частицы, движущиеся с ожидаемой скоростью), рассчитанное с помощью теории Ньютона, составляет лишь половину отклонения, наблюдаемого астрономами. Расчеты с использованием общей теории относительности намного лучше согласуются с астрономическими наблюдениями.
• В спиральных галактиках вращение звезд вокруг их центров, по-видимому, сильно противоречит закону всемирного тяготения Ньютона и общей теории относительности. Однако астрофизики объясняют это заметное явление, предполагая наличие большого количества темной материи .

Решение Эйнштейна

Часть серии по
Пространство-время
Специальная теория относительности Общая теория относительности
Концепции пространства-времени Пространственно-временное многообразие Принцип эквивалентности Преобразования Лоренца Пространство Минковского
Общая теория относительности Введение в общую теорию относительности Математика общей теории относительности Уравнения поля Эйнштейна
Классическая гравитация Введение в гравитацию Закон всемирного тяготения Ньютона
Соответствующая математика Четыре вектора Выводы теории относительности Диаграммы пространства-времени Дифференциальная геометрия Искривленное пространство-время Математика общей теории относительности Топология пространства-времени

Первые два конфликта с наблюдениями выше были объяснены общей теорией относительности Эйнштейна , в которой гравитация является проявлением искривленного пространства-времени, а не вызвана силой, распространяющейся между телами. В теории Эйнштейна энергия и импульс искажают пространство-время в непосредственной близости от них, а другие частицы движутся по траекториям, определяемым геометрией пространства-времени. Это позволило описать движение света и массы, которое согласуется со всеми доступными наблюдениями. В ОТО сила гравитации является фиктивной силой , в результате кривизны пространства — времени , так как гравитационное ускорение тела в свободном падении происходит из — за его мировая линию будучи геодезической из пространства — времени .

В чём измеряется гравитационная постоянная

Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной –

Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

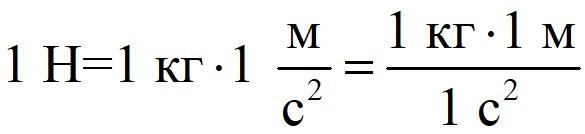
то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.

После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.

То есть единица измерения гравитационной силы –

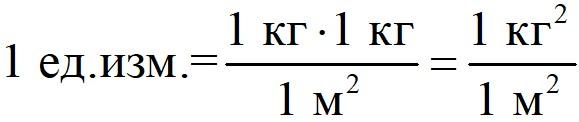
и размерность не совпадает с привычной

Проведём математические вычисления самостоятельно.

Нужно уравнять

Для этого

2 3

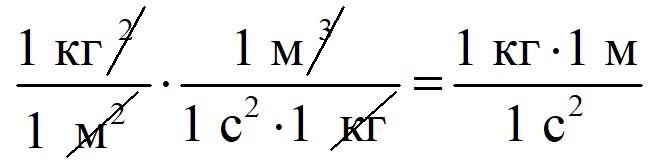
Получилась требуемая размерность.

Следовательно, постоянная имеет размерность

Вторая космическая скорость (скорость убегания)

Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т.е. удалиться на бесконечно большое расстояние от Земли.

Если:m — масса тела (кг)M — масса планеты Земля (кг)h — высота спутника над поверхностью планеты (м)rЗем — начальное расстояние между центрами масс тел (Поверхность планеты Земля) (метр)r — конечное расстояние между центрами масс тел (метр)G — гравитационная постоянная 6.67 · 10-11 (м3/(кг · сек2))U2k — вторая космическая скорость (скорость убегания)(м/c)

То кинетическая энергия тела должна быть равна работе по преодолению влияния гравитационного поля:

После упрощения и перестановки вторая космическая скорость примет вид:

Фактически вторая космическая скорость для старта ракет с поверхности планеты, это скорость которой должно обладать тело непосредственно на поверхности планеты когда h мала, а гравитационная сила велика. По мере удаления от источника гравитационной силы скорость убегания уменьшается потому, что гравитационная сила убывает, и соотвественно уменьшается необходимая для убегания кинетическая энергия.

Примечания

1. ↑ Новиков И. Д. Тяготение //Физический энциклопедический словарь. — под ред. А. М. Прохорова — М., Большая Российская энциклопедия, 2003. — ISBN 5-85270-306-0. — Тираж 10000 экз. — с. 772-775
2. Д. Д. Иваненко, Г. А. Сарданашвили Гравитация, М.: Едиториал УРСС, 2004, ISBN 5-354-00538-8
3. 10th International conference on General Relativity and Gravitation: Contribut. pap. — Padova, 1983. — Vol. 2, 566 p.
4. Тезисы докладов Всесоюзной конференции «Современные теоретические и экспериментальные проблемы теории относительности и гравитации». — М.: МГПИ, 1984. — 308 с.
5. Бутиков Е.И., Кондратьев А.С. Физика. Книга 1. Механика. — М.: Наука, 1994. — 138 с.
6. Спасский Б. И. История физики. — Т. 1. — С. 140-141.
7. Ход их рассуждений легко восстановить, см. Тюлина И. А., указ. статья, стр. 185. Как показал Гюйгенс, при круговом движении центростремительная сила F∼{\displaystyle F\sim } (пропорциональна) v2R{\displaystyle v^{2} \over R}, где v{\displaystyle v} — скорость тела, R{\displaystyle R} — радиус орбиты. Но v∼RT{\displaystyle v\sim {\frac {R}{T}}}, где T{\displaystyle T} — период обращения, то есть v2∼R2T2{\displaystyle v^{2}\sim {\frac {R^{2}}{T^{2}}}}. Согласно 3-му закону Кеплера, T2∼R3{\displaystyle T^{2}\sim R^{3}}, поэтому v2∼1R{\displaystyle v^{2}\sim {\frac {1}{R}}}, откуда окончательно имеем: F∼1R2{\displaystyle F\sim {\frac {1}{R^{2}}}}.
8. , с. 25..
9. , с. 27..
10. , с. 27—29..
11. Гинзбург В. Л. Гелиоцентрическая система и общая теория относительности (от Коперника до Эйнштейна) // Эйнштейновский сборник. — М.: Наука, 1973. — С. 63..
12. В. Паули Теория относительности, ОГИЗ, 1947
13. Фриш Д., Торндайк А. Элементарные частицы. — М.: Атомиздат, 1966. — С. 98.
14. Окунь Л. Б. Элементарное введение в физику элементарных частиц. — М.: Физматлит, 2009. — С. 105. — ISBN 978-5-9221-1070-9